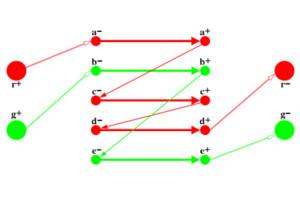
Den Ausgangspunkt der Modellierung bilden die Fahrgastfahrten und die sog. „Depots“, Gruppen als gleichartig angesehener Fahrzeuge (gleicher Typ, gleicher Betriebshof, etc.). Zu jeder Fahrgastfahrt gehört eine Gruppe zulässiger Depots, die diese Fahrt durchführen können. Fahrgastfahrten und Depots werden durch sämtliche möglichen Betriebsfahrten miteinander verknüpft. Auf diese Weise ergibt sich ein Planungsgraph, dessen Kanten und Depotgruppen die Freiheitsgrade der Planung darstellen. Umläufe entsprechen dort depotgruppenreinen Pfaden, die Zielkriterien der Umlaufplanung werden durch eine geeignete Gewichtung der Bögen implementiert. Die Umlaufplanung stellt sich damit dar als die Frage der Bestimmung einer kostenminimalen Menge von depotgruppenreinen Pfaden, so dass jede Fahrgastfahrt genau einmal überdeckt wird, ein sog. Mehrgüterflussproblem der kombinatorischen Optimierung. Mehrgüterflussprobleme sind eine im Prinzip gut untersuchte Problemklasse. Die Hauptschwierigkeit bei der Anwendung entsprechender Methoden in der Umlaufplanung liegt in der riesigen Größe der Planungsgraphen, in denen 100 Millionen und mehr mögliche Betriebsfahrten (= Freiheitsgrade!) vorkommen können. Unser Ansatz realisiert ein neuartiges Lagrangean Pricing, um diese Graphen ohne heuristische Vereinfachungen zielgerichtet zu durchsuchen. Dabei werden in einem mathematisch präzisierbaren Sinne aussichtsreiche Fahrtenverknüpfungen mit Hilfe einer Minimalkostenfluss-Relaxierung „generiert“. Die immer wieder aktualisierte Menge dieser Verknüpfungen bearbeiten wir mit LP- und Lagrange-Verfahren zur Bestimmung von unteren Schranken und als Basis für eine spezielle Heuristik zur Auflösung von Depotkonflikten zur Bestimmung von ganzzahligen Lösungen. Die Umlaufplanung ist ein kombinatorisches Problem, dass sich sehr gut zur mathematischen Optimierung eignet. Es lässt sich direkt in ein graphentheoretisches „Mehrgüterflussproblem“ übersetzen, das mit Mitteln der ganzzahligen Optimierung bearbeitet wird. Den Ausgangspunkt der Modellierung bilden die Fahrgastfahrten und die sog. „Depots“, Gruppen als gleichartig angesehener Fahrzeuge (gleicher Typ, gleicher Betriebshof, etc.). Zu jeder Fahrgastfahrt gehört eine Gruppe zulässiger Depots, die diese Fahrt durchführen können. Fahrgastfahrten und Depots werden durch sämtliche möglichen Betriebsfahrten miteinander verknüpft. Auf diese Weise ergibt sich ein Planungsgraph, dessen Kanten und Depotgruppen die Freiheitsgrade der Planung darstellen. Umläufe entsprechen dort depotgruppenreinen Pfaden, die Zielkriterien der Umlaufplanung werden durch eine geeignete Gewichtung der Bögen implemntiert. Die Umlaufplanung stellt sich damit dar als die Frage der Bestimmung einer kostenminimalen Menge von depotgruppenreinen Pfaden, so dass jede Fahrgastfahrt genau einmal überdeckt wird, ein sog. Mehrgüterflussproblem der kombinatorischen Optimierung. Mehrgüterflussprobleme sind eine im Prinzip gut untersuchte Problemklasse. Die Hauptschwierigkeit bei der Anwendung entsprechender Methoden in der Umlaufplanung liegt in der riesigen Größe der Planungsgraphen, in denen 100 Millionen und mehr mögliche Betriebsfahrten (= Freiheitsgrade!) vorkommen können. Unser Ansatz realisiert ein neuartiges Lagrangean Pricing, um diese Graphen ohne heuristische Vereinfachungen zielgerichtet zu durchsuchen. Dabei werden in einem mathematisch präzisierbaren Sinne aussichtsreiche Fahrtenverknüpfungen mit Hilfe einer Minimalkostenfluss-Relaxierung „generiert“. Die immer wieder aktualisierte Menge dieser Verknüpfungen bearbeiten wir mit LP- und Lagrange-Verfahren zur Bestimmung von unteren Schranken und als Basis für eine spezielle Heuristik zur Auflösung von Depotkonflikten zur Bestimmung von ganzzahligen Lösungen.